こんにちは総合医です。
皆さん論文を読んでいる時に箱ひげ図が出てきて読み方に困った事はありませんか?
昔一度習ってぼんやりは知ってるけど、箱ひげ図が何を示しているかを聞かれたらなかなか答えられないのではないでしょうか?
今回はそんな悩みを解決するために、箱ひげ図について解説をしたいと思います。
そもそも箱ひげ図とは
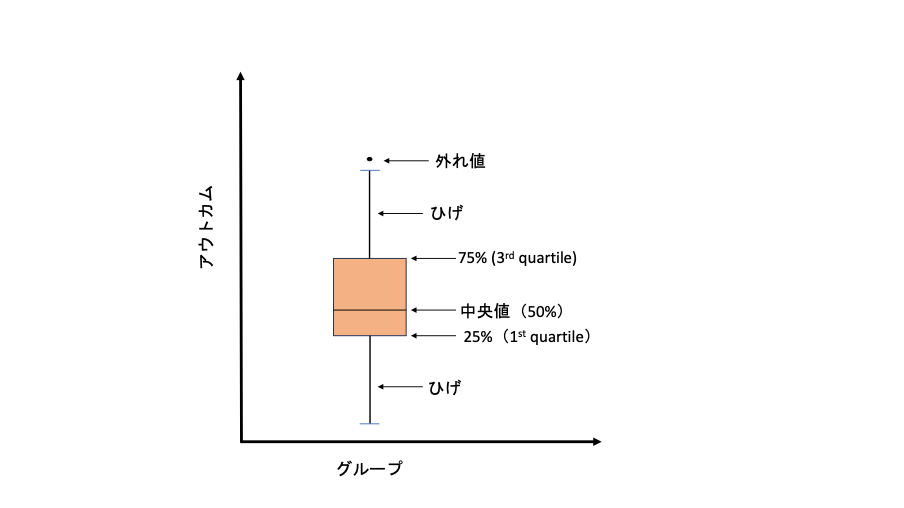
箱ひげ図とは、研究のアウトカムのばらつきを図としてわかりやすく示したものです。
研究参加者を複数に分けている場合には、グループ毎に箱ひげ図を示して、グループ間での比較も可能です。
図はアウトカムの値を縦軸、それぞれの観察グループを横軸にとって上の図のように示します。
それぞれの線は以下のものを示しています。
箱の下端の線:下から25%にいる観察値(1st quartile)がいる場所
箱の中の線 :全体の中央値、つまり下から50%の場所(2nd quartile)
箱の上端の線:下から75%にいる観察値(3rd quartile)が存在している場所
箱の上端と下の下端の間の距離:四分位範囲(Interquartile range :IQR)
箱ひげ図の場合、中央値が箱の中央に位置するとは限りません。下から数えて50%のアウトカムの場所に線が位置します。
四分位範囲(IQR)は医学研究論文でよく出てくる表現ですが、これは真ん中の50%、つまり1st quartileと3rd quartileの間の距離を示しています。
箱ひげ図のひげはこのIQRを用いて、箱の下端・上端それぞれからIQRの1.5倍の長さまで伸びています。
こうする事で、ひげで示した距離よりも中央値から外れた観察値を外れ値(Outliers)として見分けやすくしています。
ちなみにひげは英語ではWhiskerと呼ばれています。
IQRを使う利点
上で説明したように、IQRの長さをひげに適用することで、外れ値の存在を認識し、外れ値の影響を受けないように調整することができるようになっています。
なぜIQRの値を使うのかというと、多くの事象は中央値の側にアウトカムが集中し、中央値から離れるに従って観察できるアウトカムが減っていくパターンを取ることが多いです。
そのため、中央値を含んだ真ん中の50%のアウトカムを基準にそれぞれのアウトカムの影響力を考えるということをします。
もちろんアウトカムのパターンが中央値を中心として上と下にそれぞればらけていくという分布を取らないパターンも存在しているので、その時はかなり偏った箱ひげ図になったりします。
そういったデータのばらつきが一目でわかるようになっているので、データを最初に調べるときに箱ひげ図はかなり有能な図です。
IQRを基準に使う利点はもう一つあります。
それは、全体のサンプル数に影響を受けないという点です。
研究参加者の数が多すぎたり少なすぎたりする場合、外れ値として考えるのか、適切なアウトカムとして考えるのか判別困難になる事があります。
そんな時にIQRを基準に考える事で、どこまでを適切な値と捉えるのかに役立ちます。
いかがだったでしょうか。
今後論文を読んでいる時に箱ひげ図に遭遇したら、ぜひ今回の内容を思い出して、どの線が何を示しているのか、外れ値をどのように処理しているのかに着目して論文を読んでみてください。


コメント