統計② 標準偏差をどう理解したら良いのか

生物統計学を勉強し始めた時に標準偏差というものが出現し、理解に困っていませんか？

今回は標準偏差を具体的にイメージを持って理解する方法についてお話しします。

標準偏差の定義

Wikipediaでは「標準偏差とは、データや確率変数の、平均値からの散らばり具合（ばらつき）を表す指標の一つである」という説明が載っています。

そしてそれを示す式として以下のように定義されています。

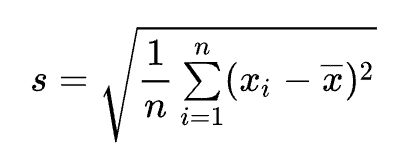
nはサンプルの数を、は平均値を示しています。

それぞれのサンプルと平均値の差の二乗を全て足し、それをサンプル数で割ってから平方根を取っています。

数学が得意な人にとっては、確かに標準偏差の定義の通り、サンプルのばらつきの平均をとったものと理解する事ができます。

しかし、平均値と聞くとすんなり理解できても、標準偏差を使った事がある人は少数派でしょうし、すんなりそのまま腹落ちする人は少ないと思います。

それではどのように理解すれば良いのでしょうか？

標準偏差が話題に出る時は、主に正規分布という釣鐘型の図と一緒に使用される事が多いです。

正規分布とは、確率分布とも呼ばれ、いろいろな事象で自然に出来上がる分布をグラフで示したものです。

特徴としては、真ん中が平均値となっており、平均値から離れるほど分布が減っていき、左右対称になっています。

自然界の多くの事象でこの分布は当てはまっており、ランダムに人間を選ぶと、身長、体重、IQなど全てこの正規分布に沿った形で分布します。

統計学を学ぶとき、この正規分布に沿って物を考える事が多くあるのですが、残念ながらこの正規分布というのはいつも一定の形をしているわけではありません。

調べるものによっては、細い釣鐘になることもあれば、太い釣鐘になる時もあり、グラフの幅が変化します。

そんな時に今回お話ししている標準偏差というのが大事になってきます。

標準偏差が正規分布の釣鐘の幅を教えてくれる指標となっており、正規分布を利用した統計学的な解析は必ず標準偏差の値が関わってきます。

正規分布の形は、中心の値と標準偏差で決まるので、正規分布の話をする時にはこの２点をしっかりと確認しましょう。

標準偏差が正規分布の釣鐘の幅に関わっているのはわかったけど、どのように理解すれば良いのかというと、正規分布の特徴として、１標準偏差の中に６８％のサンプルが含まれるというものがあります。

そのため、平均値の周辺で６８％のサンプルが含まれる幅を標準偏差という事ができます。

６８％が少し中途半端には聞こえますが、１標準偏差がどの程度の幅と対応しているのかと考えるとグッと理解しやすくなるのではないでしょうか？

医学論文では９５％信頼区間という物をよく目にしますが、９５％のサンプルが含まれる幅も標準偏差を使う事で示すことができ、その値は１.９５標準偏差になっています。

９９％のサンプルを含みたい場合は２.５８標準偏差の幅に含まれます。

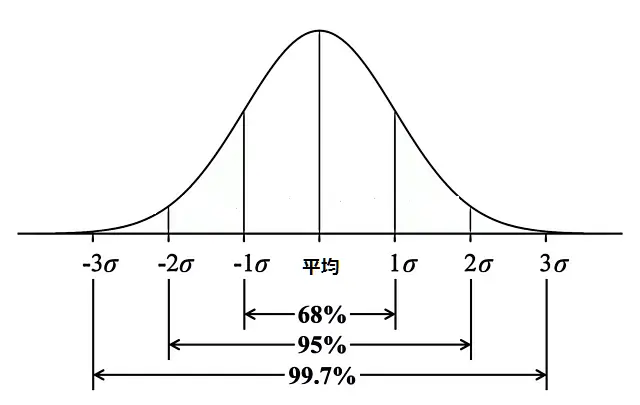
そして正規分布を想定した統計解析は、この１.９５標準偏差という数値を用いて９５％信頼区間を計算しています。

この何%のサンプル数が含まれる幅という考え方が標準偏差を理解する上で一番重要な事だと思います。

次回標準偏差というワードが出てきた時はぜひこの考え方を使ってみてください。